Welcome to Representing Knowledge with Primitives
Computers should help people deal with everyday problems
from making decisions to playing games.
To offer more help,
computers need more complete representations of
knowledge,
defined as useful incorporated information.
This web site provides tools to collaborate on
creating more complete representations,
starting with textual natural language.
Hypothesis
This research web site explores an integration hypothesis about
representing knowledge.
The integration is novel,
most likely transformational,
addressing many issues of older approaches known as
Symbolic Artificial Intelligence.
- Conditional probabilities
- Conditional probabilities
deal with uncertainty in information,
ambiguity, vagueness, and approximation.
Probabilities
factor in utilities,
which principled Decision-Analytics may use to choose the best
among an exponential quantity of processing alternatives.
Probabilities
subsume other uncertainty measures and include
higher-order probabilities
about the measures themselves.
- with
closure logic expressions
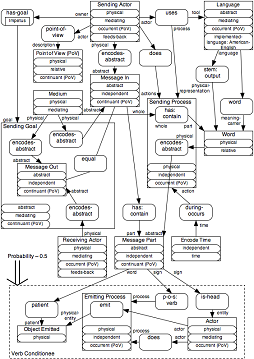
- To get an expressive and fine-grained enough representation,
conditional probabilities,
which are statements about events,
can use complex logic expressions, including
closure logic.
Closure logic
can express negation and the stop words that other approaches ignore.
Providing a unified methodology,
closure logic
can express intent, including subjunctive hypotheticals,
along with other moods without using modal logic;
processes; and contexts like frames.
- with predicates from a limited set of
primitives
- Predicates in
closure logic expressions
can come from a limited set of templates, called
primitives,
which parameterize values, e.g., numbers and strings.
Specific to generic hierarchies among conditions can
derive taxonomies.
Expressions can be compared and manipulated to handle analogies.
- can tractably represent common sense knowledge.
- This combination should lead to new processing capabilities,
despite the unbounded nature of ideas, the complexity of ideas,
and the uncertainty of the ideas communicated with natural language.
Tractable means easily managed or controlled (probabilistic)
rather than running in polynomial time (deterministic).
Benefits
Knowledge Representations drive the implementations
of general purpose computing, called Artificial Intelligence
as it approaches human capabilities.
An implementation of the hypothesis can satisfy
goals for Knowledge Representation of being:
helpful, understandable, principled, parsimonious, small, and secure.
Many classes of use cases could employ this implementation:
- Assessment: Personal information management, Inference, Diagnosis,
Situation assessment, Monitoring, Traditional learning
- Decisions: Decision support, Automated decision making, Planning,
Integrated applications
- Language: Information retrieval, Summarization, Web understanding,
Document editing, Translation
- Development: Development management, Automated development,
Program synthesis
- Perception: organizing sensor input
- Novelty: Analogy, Creativity, Problem solving
An implementation of the hypothesis could support several requirements
that can be derived from these use cases:
capability, access, context, uncertainty, judgment, adaptability, efficiency,
and possibly scale.
The comparison of methods
page gives more details.
Describing applications
that go well beyond what is currently possible using a developing technology
that mostly correctly recognizes text
and provides a representation of its meaning
that may be reasoned about, including uncertainties, is a challenge.
With such applications in mind,
collaborators or other help could develop the technology more quickly.
Approach
The Knowledge Representation implementation proper supports a text
natural language understanding
(NLU) system,
which includes skills and interfaces of a model-controller-view architecture.
The implementation wraps temporary working and persistent databases
with semantic capabilities.
Other routines, called Skills here,
access those capabilities, themselves, and
interfaces to users and other data.
The Knowledge Representation development approach includes:
The approach provides several implementation benefits.
- Compact
- Only a few kinds of components produce the entire Knowledge Representation:
Conditional probabilities containing
closure logic
expressions have predicates with unbounded parameters (numbers, strings)
from limited set of primitives (predicate patterns),
combined in
closures
only with conjunctions (AND) and classical negation (NOT).
Other commonly used
logic
components such as functions, constants,
disjunctions (OR), implications, or modals (possibility, deontic logic)
may be constructed from the few.
A common representation allows diverse items,
such as meanings, syntax, and processing actions,
to be combined, which has been a long-standing issue
for natural language understanding.
Having few component types also simplifies implementation,
nonetheless allowing specializations and heuristics to optimize processing.
- Comprehensive
- A few, well-chosen components can represent much.
Taxonomies of ontologies
derive
from combining components.
Contexts are the closures of
closure logic.
Conditional probabilities
can potentially have multiple meanings simultaneously,
such as the connotations and denotations of words, the meat of logic.
Closures
that subtract predicates can represent metaphors.
Closures may explicitly represent paradoxes
even though they are inconsistent in traditional logic.
Closures
also easily attach metadata to statements.
Rare events, counterfactuals, and fiction need nothing special.
- Clear
- The few declarative components provide clarity.
Information coming from the approach
has a straightforward explanation with logic,
which may be resistant to bias or misinformation.
The conditional probabilities and their expressions
have graphical representations providing alternates to pure, linear symbols.
There is not even a
Rete algorithm
to complicate explanation.
- Optimizable
- The approach allows optimizing representation.
Among uncertainty measures,
probabilities
permit great accuracy allowing modeling of phenomena
from measurements like frequencies to subjective judgments.
Secondary (higher-order) probabilities,
as I. J. Good discussed,
allow the explicit representation of precision.
Probabilities
provide a rich collection of manipulations
including conditional probabilities.
With probabilities and value judgments,
Decision Theoretic techniques can both justify external judgments
and provide a rational for internal processing decisions.
The fine-grained components may attach specializations and heuristics
for more efficient processing.
The processing cycles used should be orders of magnitude less than
current popular approaches.
- Flexible
- The approach is flexible both in how it is used and how it is implemented.
The conditions of conditional probabilities
linked into a generic and specific hierarchy provides defaults.
Each situation can override the defaults,
allowing custom handling, for instance, for different users.
These defaults allow defeasible non-monotonic reasoning
providing real-time knowledge maintenance.
The set of suggested primitives in use is not gospel.
Although some primitives are unlikely to change,
in particular, those that John F. Sowa
suggests,
many of the suggested primitives may easily be substituted,
at least initially.
- Extensible
- The approach includes capabilities for extensions.
The implementation being developed includes algorithms for
the maintenance of conditional probabilities organized by condition.
Conditions may be created with their conditionees (outcomes),
replaced as conditions or with their conditionees, updated,
and deleted (CRUD), the standard for database operations.
A heuristic merging algorithm will suggest combined
closure logic
expressions for either the conditions or conditionees.
These algorithms form the basis for other extensions
such as rules engines, which may be implemented with theorem provers.
Since the approach does not implement arithmetic and statistics,
such capabilities could be implemented as added layers.
Handling of natural language,
possibly including tokenization; stemming or lemmatization;
parsing, which could look up appropriate syntax, including suffixes;
and generation, which could weigh and select attributes arranged for output
could also be capabilities that would access the representation.
Other capabilities, for instance creating computer programs,
might also have an implementation that accessed the representation.
Getting started
Collaborators are welcome to add their thoughts about how
anything may be described.
Such philosophical insights may be given without specific consideration
of the closure logic,
probabilities,
or algorithms that handle them.
Register to read more.
Then make an edition to collaborate.
As desired, add primitives or
condition groups
with outcomes.
This introduction,
comparison of methods,
glossary,
references,
and site implementation
pages are openly available.
However, most pages are only available to registered collaborators.
Collaborators register
with the site providing at least postal codes,
such as a U.S. ZIP code,
which provides a locality, and
E-mail addresses so that a site administrator may authenticate them.
Since authentication is manual,
new potential collaborators may gain full access slowly,
particularly if the information provided is minimal.
Except for a self-assigned identifier string,
all collaborator information is only available to administrators,
unless collaborators choose to share their information
with other authenticated collaborators.
Only a few pages are visible without logging in.
Copyright © 2022
Robert L. Kirby.
All rights reserved.